


Next: About this document ...
A CYK algoritmusról tényleg nagyon röviden
Az algoritmus egy alulról felfele történő elemzést valósít meg.
Ahhoz, hogy
működjön az kell, hogy a nyelvtan Chomsky normál alakban (CNF)
legyen, azaz
a nyelvtanban csak
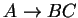 illetve
illetve
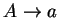 szabályok vannak (meg
esetleg az
szabályok vannak (meg
esetleg az
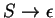 ,
de az most úgysem játszik).
Ha egy n hosszú
,
de az most úgysem játszik).
Ha egy n hosszú
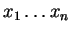 (ahol xi-k a betűk)
szót szeretnénk elemezni, akkor egy nxn-es
alsó háromszög
mátrix alakú táblázatot fogunk kitölteni a következő módon.
A sorokat alulról felfele számozzuk, az oszlopokat balról jobbra.
Az i. sor j. kockájába akkor kerül a A nemterminálisa a
nyelvtannak, ha az A-ból levezethető az elemzendő input szó
azon darabkája, ami a j. betűnél kezdődik és i hosszan tart, vagyis
levezethető az
(ahol xi-k a betűk)
szót szeretnénk elemezni, akkor egy nxn-es
alsó háromszög
mátrix alakú táblázatot fogunk kitölteni a következő módon.
A sorokat alulról felfele számozzuk, az oszlopokat balról jobbra.
Az i. sor j. kockájába akkor kerül a A nemterminálisa a
nyelvtannak, ha az A-ból levezethető az elemzendő input szó
azon darabkája, ami a j. betűnél kezdődik és i hosszan tart, vagyis
levezethető az
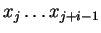 részszó.
Ha kitöltjük a táblázatot és a legfelső mezőben szerepel a
mondatszimbólum S az azt jelenti, hogy S-ből levezethető
a szó az első betűtől az n.-ig, vagyis végig.
részszó.
Ha kitöltjük a táblázatot és a legfelső mezőben szerepel a
mondatszimbólum S az azt jelenti, hogy S-ből levezethető
a szó az első betűtől az n.-ig, vagyis végig.
Ha az S nem jelenik meg a legfelső kockában, akkor a szó nem
eleme a nyelvnek.
A táblázat kitöltése:
Az első sor egyértelmű: azok a nemterminálisok kerülnek a k.
mezőbe, akik egy lépésben a k. terminálist generálják egy
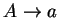 alakú szabállyal.
alakú szabállyal.
Későbbi sorok: egy A akkor lesz az i. sor j. oszlopában, ha
belőle levezethető az
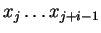 szó.
Mivel csak
szó.
Mivel csak
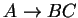 alakú szabályok vannak ezért ez csak úgy lehet,
hogy a B megcsinálja
alakú szabályok vannak ezért ez csak úgy lehet,
hogy a B megcsinálja
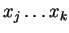 -t (az elejét, valameddig), a C
pedig
-t (az elejét, valameddig), a C
pedig
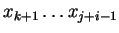 -et (a maradékot).
De ezt már le lehet ellenőrizni,
mert ezek az információk a táblázat már kitöltött részében benne
vannak. Tehát egy A-t akkor írunk be az i. sor j. kockájába,
ha van
olyan
-et (a maradékot).
De ezt már le lehet ellenőrizni,
mert ezek az információk a táblázat már kitöltött részében benne
vannak. Tehát egy A-t akkor írunk be az i. sor j. kockájába,
ha van
olyan
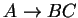 szabály, hogy B benne van a j. oszlop k. sorában valami
k-ra, a C meg benne van a k+1. oszlop i-k. sorában.
szabály, hogy B benne van a j. oszlop k. sorában valami
k-ra, a C meg benne van a k+1. oszlop i-k. sorában.
Ha nem csak arra vagyunk kíváncsiak, hogy generálni lehet-e a szót,
hanem arra is, hogy hogyan, akkor nem csak a megfelelő nemterminálist
írjuk be a táblázatba, hanem ellátjuk két indexszel is: az első
mutatja, hogy milyen felbontásban generálja a BC sorozat a
szórészletet (azaz, hogy a B hány darab betű generál, ez a fenti
jelölésekkel a k),
a második meg a szabálynak a szám, amit használunk (vagyis az
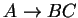 szabály sorszáma, a szabályokat még az elején megszámoztuk, hogy
lehessen rájuk hivatkozni). Az első index tulajdonképpen azt mutatja,
hogy az így beírt A oszlopában hányadik sorban kell keresnünk a B-t,
a szabály száma meg azt mutatja, hogy mit is kell keresnünk.
Így a levezetési fa felépíthető. Ha ezen visszakeresés során elágazást
tapasztalunk (azaz van olyan kocka, ahol két ugyanolyan, de más indexű
nemterminális áll), akkor a szó nem egyértelműen áll elő.
Ekkor a visszakeresős eljárás mindkét levezetési fát megadja.
szabály sorszáma, a szabályokat még az elején megszámoztuk, hogy
lehessen rájuk hivatkozni). Az első index tulajdonképpen azt mutatja,
hogy az így beírt A oszlopában hányadik sorban kell keresnünk a B-t,
a szabály száma meg azt mutatja, hogy mit is kell keresnünk.
Így a levezetési fa felépíthető. Ha ezen visszakeresés során elágazást
tapasztalunk (azaz van olyan kocka, ahol két ugyanolyan, de más indexű
nemterminális áll), akkor a szó nem egyértelműen áll elő.
Ekkor a visszakeresős eljárás mindkét levezetési fát megadja.
Egy példa végigszámolva, magyarázatokkal itt.



Next: About this document ...
Judit Csima
2000-04-13