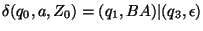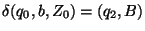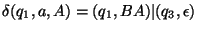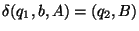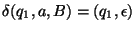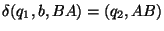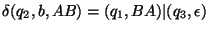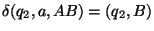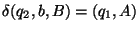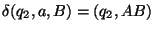1. Az aritmetikai kifejezések általunk megszokott infix jelölése helyett sokkal célszerűbb a prefix vagy posztfix lengyel jelölés használata. Például a csak összeadást és szorzást használó posztfix lengyel aritmetikai kifejezéseket az alábbi nyelvtan generálja: $E\ensuremath{\rightarrow} EE+\vert EE*\vert a.$ Készítsen nyelvtant, ami az $\cup$ (vagy), $\cap$ (és) diadikus, illetve $\neg$ (negálás) monadikus operátorokkal adott posztfix jelölésű kifejezéseket generálja. Adja meg a nyelvtant GNF-ban is, majd adja meg az $aaa\neg a \cap \cup \cap a \neg \cap$ kifejezés levezetési fáját mindkét nyelvtanban. 2. Egy nyelv egy G1 nyelvtana lefedi a nyelv egy G2 nyelvtanát, ha a nyelv minden szavára igaz, hogy minden, a G2 nyelvtannal előállított lefezetési fa megkapható a G1-hez tartozó levezetési fából összevonásokkal. Összevonás alkalmával a fa valamelyik ágát egy ponttá húzzuk össze. Adott egy nyelv egy nyelvtana. Ebből elkészítjük a CNF és a GNF alakú nyelvtanokat. Mikor igaz, hogy az így kapott nyelvtanok lefedik az erdetit? 3.Mit generálnak az alábbi nyelvtanok? Egyértelműk-e a nyelvtanok? $S\ensuremath{\rightarrow} aSb\vert\epsilon$ $S\ensuremath{\rightarrow} SaSb\vert\epsilon$ $S\ensuremath{\rightarrow} aSbS\vert\epsilon$ $S\ensuremath{\rightarrow} SaSbS\vert\epsilon$ $S\ensuremath{\rightarrow} SaSaSb\vert\epsilon$ 4. Egy nyelv szavai az a karakterrel kezdődnek, b-vel végződnek, az ábéce az $\{a,b\}$. Ha egy teljes homogén a sorozat páros, akkor az azt követő teljes homogén b sorozat eggyel rövidebb hosszú, mint az a sorozat volt, míg ha az a sorozat pártalan, akkor a b-s sorozat eggyel hosszabb. Nyelvtan és automata kell. 5. Automata kell: $\{a^ib^jc^k\;\vert\;i+k=j\geq 0\;\}$ 6. PDA kell a következő nyelvhez: $\{a^mb^n\;\vert\;m\leq n\leq 2m\;\}$ 7. PDA kell ahhoz a nyelvhez, melynak ábécéje az $\{a,b\}$ és szavaiban az a és a b karakterek száma megegyezik. 8. Legyen egy röntgenszemű automata szabályrendszere a következő: $\delta(q_0,a,Z_0)=(q_1,BA)\vert(q_3,\epsilon)$ $\delta(q_0,b, Z_0)=(q_2,B)$ $\delta(q_1,a, A)=(q_1,BA)\vert(q_3,\epsilon)$ $\delta(q_1,b,A)=(q_2,B)$ $\delta(q_1,a,B)=(q_1,\epsilon)$ $\delta(q_1,b, BA)=(q_2,AB)$ $\delta(q_2,b, AB)=(q_1,BA)\vert(q_3,\epsilon)$ $\delta(q_2,a, AB)=(q_2,B)$ $\delta(q_2,b,B)=(q_1,A)$ $\delta(q_2,a, B)=(q_2,AB)$ Szerkesszen egyenértékű szokásos automatát és adja meg az elfogadott nyelvet!