|
A táblázatok:
| Semmi = 0 |
b = 1 |
d = 2 |
| |
|
|
 |
 |
 |
| |
 |
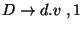 |
| |
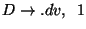 |
|
| |
|
|
| v = 3 |
u = 4 |
v = 5 |
| |
|
|
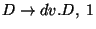 |
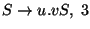 |
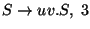 |
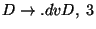 |
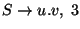 |
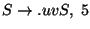 |
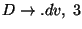 |
|
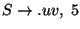 |
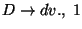 |
|
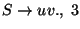 |
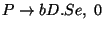 |
|
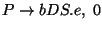 |
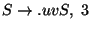 |
|
|
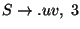 |
|
|
| |
|
|
| u = 6 |
v = 7 |
e = 8 |
| |
|
|
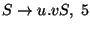 |
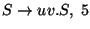 |
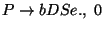 |
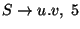 |
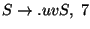 |
|
| |
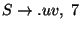 |
|
| |
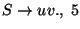 |
|
| |
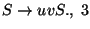 |
|
| |
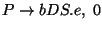 |
|
| |
|
|
A táblázatokból visszakereséssel jön a levezetési fa: visszanézzük, hogy melyik
szabály miért került be a táblákba.
Hátulról kezdjük: az utolsó táblában a
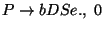 a 7. táblában
levő
a 7. táblában
levő
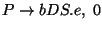 miatt jött be.
A miatt jött be.
A
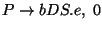 szabály azért került be, mert ugrottuk az S-t, azt meg
azért tettük, mert az
szabály azért került be, mert ugrottuk az S-t, azt meg
azért tettük, mert az
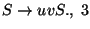 szabály végére értünk, annak meg azért értünk
a végére, mert az
szabály végére értünk, annak meg azért értünk
a végére, mert az
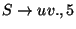 szabálynak a végére értünk.
Satöbbi, satöbbi...
Így visszajutunk és közben építjük a fát. Mire az elejére érünk, az első táblához,
addigra teljes lesz a fa.
szabálynak a végére értünk.
Satöbbi, satöbbi...
Így visszajutunk és közben építjük a fát. Mire az elejére érünk, az első táblához,
addigra teljes lesz a fa.
|